Correção de atividades do livro APROVA BRASIL - Editora Moderna - LIÇÃO 5: Diferentes representações de um número

 COMPONENTE CURRICULAR: MATEMÁTICA

PROFESSOR: WIVIAN FÉLIX     

TURMA: 62.01

Correção de atividades do livro APROVA BRASIL - 

Editora Moderna

LIÇÃO 5 - p. 42 a 49

 ATIVIDADE 1

Compreenda
a) Qual é a tarefa proposta na atividade?
Determinar quem comprou menos carne no açougue, quem conseguirá fazer
mais quibes e o número de quibes que serão feitos a mais. 

b) Que frações aparecem na atividade?

c) O que representam essas frações?
Representam a quantidade de carne que Joana, Alice e Beatriz compraram  

d) Quanto mais carne for comprada, será possível fazer mais ou menos quibes?
Com mais carne será possível fazer mais quibes  

Responda  

Agora, represente na forma decimal cada uma das frações mencionadas na atividade 

b) Com base na resposta ao item anterior, responda à primeira questão da atividade.
Beatriz comprou menos carne. 

c) Se com 1 kg de carne é possível fazer 10 quibes, quem comprou mais carne poderá fazer quantos quibes?
Como Joana comprou 1,5 kg de carne, poderá fazer 15 quibes.

d) Preencha a frase com a resposta à segunda questão da atividade.
Joana fará mais quibes. Serão 15 quibes no total 

ATIVIDADE 2:

Compreenda
a) Qual é a tarefa proposta na atividade?
Determinar a fração do total de pinos que cada jogador derrubou na primeira
rodada do jogo de boliche e quantos pinos foram derrubados por cada um nessa rodada.

b) Quantos são os jogadores? Quem são eles?
Há 6 jogadores: Bernardo, Fernando, Samuel, Leila, Bárbara e Gabriela  

c) Quantos pontos cada jogador fez na primeira rodada?
Bernardo: 0,9; Fernando: 0,3; Samuel: 0,6; Leila: 0,7; Bárbara: 0,8; e Gabriela: 1,0.

d) Quem fez mais pontos? Quantos pontos esse jogador fez?
Gabriela teve a maior pontuação, totalizando 1,0 ponto  

Responda
a) Leia a informação a seguir.

O número 0,1 pode ser representado na forma de fração decimal por 10 1 . Do mesmo
modo, o número 0,3 pode ser representado na forma de fração decimal por 10 3 .

• Como você representaria, na forma de fração decimal, a quantidade
de pinos que Bernardo derrubou na primeira rodada?  

b) Indique a fração decimal do total de pinos que cada jogador derrubou
para responder ao primeiro item da atividade 

c) Quantos pinos cada jogador derrubou?
Bernardo derrubou 9 pinos; Fernando, 3; Samuel, 6; Leila, 7; Bárbara, 8; e Gabriela, 10.  

ATIVIDADE 3

 Compreenda

a) O que é proposto na atividade?
Identificar a fração que representa a parte colorida de todas as figuras juntas;
verificar se essa fração pode ser representada na forma mista; localizar entre quais números
naturais e consecutivos o número racional representado por essa fração está localizado.

b) Quantas figuras foram apresentadas na atividade?
Foram apresentadas 3 figuras.

c) Em quantas partes cada figura está dividida?
Cada figura está dividida em 5 partes.

d) Identifique quantas são as partes coloridas em cada figura.
As figuras 1 e 2 têm 5 partes coloridas, e a figura 3 tem 3 partes coloridas. 

Responda
a) Que fração representa a menor parte de cada figura em relação
à figura toda?

b) Que fração representa a parte colorida de cada uma das figuras?

c) Com as frações representadas no item anterior, responda à primeira questão da atividade.

• Que fração representa a parte colorida de todas as figuras juntas? 

 

d) Essa fração pode ser representada na forma mista?

e) Determine a forma decimal da fração e verifique entre quais números naturais consecutivos ela está situada para responder à última questão da atividade.

13: 5 = 2,6

A fração está situada entre os números 2 e 3  

ATIVIDADE 4

Compreenda 

a) Qual é a tarefa proposta na atividade?
Determinar a representação decimal dos números que devem ser localizados na
reta numérica; verificar se Pedro localizou os números corretamente e, caso tenha errado,
indicar o erro.

b) Quais números a professora pediu que fossem localizados na reta numérica?  

c) Quais são os números inteiros que aparecem na reta numérica?
Aparecem os números 0, 1, 2, 3 e 4.

d) Em quantas partes estão divididos os intervalos entre os números inteiros da reta numérica?
Os intervalos entre os números inteiros estão divididos em 4 partes  

Responda

a) Que números racionais, representados na forma de fração, podem ser localizados nas partes que dividem o intervalo entre os números 0 e 1?

Indique na reta abaixo  

b) Os números que a professora pediu que fossem localizados na reta numérica são maiores ou menores que as frações indicadas no item anterior?
São maiores que as frações do item anterior.

c) Represente os números da atividade na forma decimal para responder à primeira questão da atividade.  

d) Com base na resposta anterior, localize os números na reta numérica e responda à segunda questão

da atividade.

Pedro não localizou todos os números de forma correta. Ele errou na indicação dos números

  

AULA DE MATEMÁTICA COM MATERIAL DOURADO

SÉRIE: 6º ANO

Uso do material dourado, para trabalhar quadrados perfeitos e radiciação.

CINEMÁTICA - CONCEITOS INICIAIS

    Os movimento dos corpos são estudados em uma área da Física denominada Cinemática, que os descreve sem se preocupar com suas causas.

Para o estudo da Cinemática, é fundamental compreender alguns conceitos básicos:

MOVIMENTO E REPOUSO (https://www.youtube.com/watch?v=bi86esjeAA4)

REFERENCIAL = ponto, objeto ou sistema que é utilizado para definir a posição e o estado de movimento ou repouso dos demais objetos

Um objeto está em MOVIMENTO em relação a um referencial quando a sua posição muda ao longo do tempo.

Um objeto está em REPOUSO em relação a um referencial quando sua posição permanece constante  em relação ao longo do tempo.

ATIVIDADES

1. Neste momento, seus livros e cadernos, em relação à mesa em que estão apoiados, encontram-se em movimento ou em repouso? Por quê?

2. Se um corpo está em movimento em relação a certo referencial, ele está em movimento em relação a qualquer referencial? Justifique sua resposta.

3. Duas amigas, Renata e Bárbara, passeiam de bicicleta e pedalam próximas para poderem conversar, mantendo a velocidade constante e igual. Com relação à situação descrita, defina o estado de movimento ou repouso para: 

a) Bárbara em relação ao solo:

b) Renata em relação ao solo:

c) Bárbara em relação a Renata: 

d) Renata em relação a Bárbara:

e) Bárbara em relação ao Sol:

f) Renata em relação à bicicleta:

4.Em um passeio de carro de Arraias, uma pessoa comenta: "O Campus da UFT chegará até nós em 15 minutos".

a) Qual o referencial adotado?

b) Reescreva a frase considerando como referencial o Campus da UFT.

5. Se um corpo está em movimento em relação a um corpo B, e B está em movimento em relação a um corpo C, A está em movimento em relação a C. Julgue essa afirmação, classificando-a como verdadeira ou falsa, e forneça um exemplo que justifique sua resposta.

 TRAJETÓRIA

A Trajetória é a linha determinada pelas sucessivas posições ocupadas pelo corpo no decorrer de um intervalo de tempo em relação ao referencial.

A trajetória não é uma grandeza, mas sim uma propriedade dos movimentos. Por esse motivo, ela não pode ser medida, nem tem uma unidade de medida.

As ´principais classificações da trajetória são:

ATIVIDADES

1. Classifique a trajetória em cada uma das situações a seguir.

a) O movimento das pás de um ventilador em relação a uma pessoa parada.

b) O movimento da Terra em torno do Sol, em relação ao Sol.

c) O chute de tiro de meta em uma partida de futebol em relação a um torcedor que assiste ao jogo da arquibancada.

d) A trajetória dos atletas em uma corrida de 100 metros em relação à pista.

2. Um adolescente está andando de skate enquanto lança uma chave para cima. Considerando que a sua velocidade seja constante, determine o formato da trajetória:

a) da chave em relação a um observador que vê a situação lateralmente;

b) da chave em relação ao adolescente;

c) do adolescente em relação ao skate;

d) do adolescente em relação ao solo;

3. Um avião voa com velocidade constante e abandona uma caixa de alimentos. Desprezando a resistência do ar, qual será a trajetória executada pela caixa em relação:

a) a um observador fixo no solo;

b) a um observador no avião;

4. Um parafuso se desprende do teto de um ônibus que está em movimento, com velocidade constante em relação a Terra. Desprezando a resistência do ar, a trajetória do parafuso, em relação ao ônibus, é:

a) parabólica.

b) retilínea e vertical.

c) um ponto geométrico.

d) retilínea e horizontal.

e) inclinada

GRANDEZAS E UNIDADES

    Grandezas Físicas são propriedades da natureza que podem ser medidas e comparadas numericamente com um padrão preestabelecido, como comprimento, tempo, massa, velocidade e aceleração.

         Para medir uma grandeza física é necessário primeiramente definir o padrão de medida a ser adotado. Ao medir a largura de uma mesa (ou carteira), pode-se utilizar como padrão de medida, por exemplo, o tamanho de uma caneta. No entanto, como as canetas têm tamanhos diferentes, as medidas de largura da carteira podem apresentar diferentes valores de acordo com a caneta utilizada.

MEDIDAS DE COMPRIMENTO

MEDIDAS DE MASSA 

Medidas Especiais:

1  tonelada (T) = 1000 kg

         1 arroba  = 15 kg

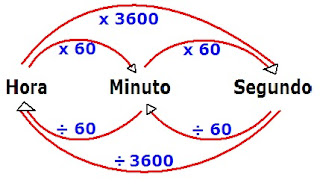
MEDIDAS DE TEMPO

OUTRAS UNIDADES DE TEMPO

1 dia = 24 horas

1 semana = 7 dias

1 quinzena = 15 dias

1 mês = 30 dias

1 semestre = 6 meses

1 bimestre = 2 meses

1 trimestres = 3 meses

1 ano = 12 meses = 365 dias

ATIVIDADES

1. O que são grandezas físicas? Cite pelo menos três exemplos de grandezas utilizados frequentemente em seu dia a dia.

2. Marque com X as propriedades a seguir que podem ser consideradas grandezas físicas.

a) (    ) Beleza

b) (    ) Volume de um copo

c) (    ) Felicidade

d) (    ) Massa de uma pessoa

e) (    ) Tempo

f) (    ) Velocidade de um carro

g) (    ) Aresta de um cubo

h) (    ) Cansaço

3. As primeiras unidades de comprimento tinham como referência o corpo humano e seus membros. Explique por que o uso do corpo humano e de seus membro pode tornar as medições imprecisas e  confusas?

4. Utilizando as unidades de comprimento e as unidades de massa, estime a unidade mais adequada para medir:

a) a massa de um comprimido;

b) a massa de uma pessoa;

c) a distância entre duas cidades;

d) a massa de um caderno;

e) o diâmetro de um bastão de grafite;

f) a altura de uma pessoa;

g) o comprimento de um caderno;

h) a massa de um cachorro;

5. Realize as transformações adequadas entre as unidades de medida.

a) 360 s = _________min

b)  48 s = __________ min

c) 3 anos = _________ h

d) 120 cm = ________ m

e) 1400 mg = ________ g

f) 22 arrobas = _______ kg

g) 480 h = ______ dias

h) 1,5 h = ______ s

i) 2,2 km = ______ m

j) 0,12 m = ______ cm

k) 2,5 T = _____ kg

l) 0,13 kg = ______ g

m) 36 min = _______ h

n) 12 dias = _____ h

o) 350 m = ______ km

p) 250 g = ______ kg

q) 89 kg = ______ T

r) 2,4 g =  ______ mg

RESOLUÇÃO DE PROBLEMAS - ÁREA DE FIGURAS PLANAS

                                                 EXERCÍCIOS

1. Determine a área de uma sala quadrada, sabendo que a medida de seu lado é 6,45 m.

2. Vamos calcular a área de uma praça retangular, em que o comprimento é igual a 50 m e sua largura mede 35,6 m.

3. Calcule a área de um retângulo, em que a base mede 34 cm e sua altura mede a metade da base.

4. É necessário um certo número de pisos de 25 cm x 25 cm para cobrir o piso de uma cozinha com 5 m de comprimento por  4 m de largura. Cada caixa tem 20 pisos. Supondo que nenhum piso se quebrará durante o serviço, quantas caixas são necessárias para cobrir o piso da cozinha?

5. Quantos metros de tecido, no mínimo, são necessários para fazer uma toalha para uma mesa que mede 300 cm de comprimento por 230 cm de largura?            

6. Um pintor foi contratado para pintar uma sala retangular que mede 5,5 m x 7 m. Para evitar que a tinta respingue no chão ele vai forrar a sala com folhas de jornal. Quantos metros de folha de jornal ele vai precisar?

7. Vamos calcular a área de um losango, sabendo que sua diagonal maior mede 5 cm e a diagonal menor mede 2,4 cm.

8. Sabendo que a base maior de um trapézio mede 12 cm, base menor mede 3,4 cm e sua altura mede 5 cm. Calcule a área deste trapézio.

TESTES 

1. Um empresário possui um espaço retangular de 110 m por 90 m para eventos. Considerando que cada metro quadrado é ocupado por 4 pessoas, a capacidade máxima de pessoas que esse espaço pode ter é:

a) 32.400                  

b) 34.500       

c) 39.600         

d) 42.500        

e) 45.400

2. Os pontos (2,3), (5,3) e (2,7) são vértices de um triângulo retângulo. A área desse triângulo é:

a) 5 u.a              

 b) 6 u.a           

c) 7 u.a         

d) 8 u.a

e) 9 u.a

3. Ricardo esteve em um lançamento imobiliário onde a maquete, referente aos terrenos, obedecia a uma escala de 1:500. Ricardo se interessou por um terreno de esquina, conforme mostra a figura da maquete.

A área, em metros quadrados, desse terreno é de

(A) 300.

(B) 755.

(C) 120.

(D) 525.

(E) 600.

4. 

QUESTOES DESCRTORES - ADA

EXERCICIOS - PERIMETRO DE FIGURAS PLANAS

1) Calcule o perímetro da figura abaixo:

2) Calcule o perímetro da figura abaixo:

3) Se o perímetro de um quadrado é de 64 cm, qual é a medida de cada lado desse quadrado?

4) Um fazendeiro pretende cercar um terreno retangular de 120 m de comprimento por 90 m de largura. Sabe-se que a cerca terá 5 fios de arame. Quantos metros de arame serão necessários para fazer a cerca? Se o metro de arame custa R$ 15,00, qual será o valor total gasto pelo fazendeiro?

5) O perímetro de um retângulo mede 92 cm, quais são suas medidas, sabendo-se que contem 8cm a mais que a largura? Calcule.